1. 서론
지금 당장 구글에 세상에서 가장 아름다운 수식을 검색해보면
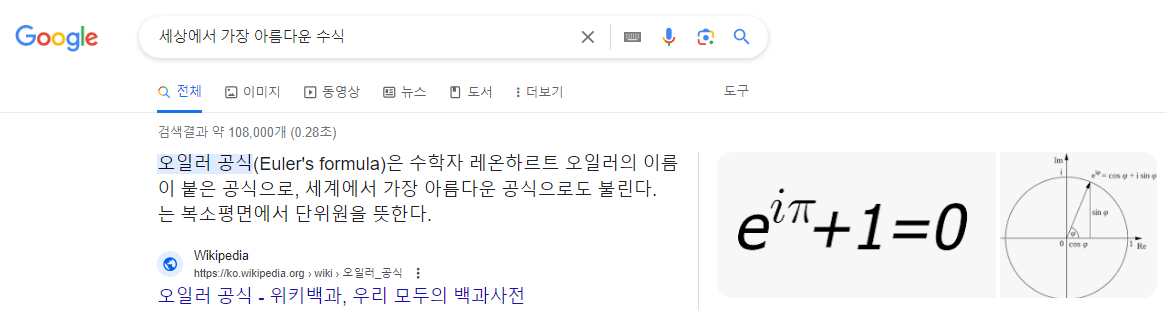
오일러 공식이 가장 아름다운 수식이라 주장합니다. 믿을 수 없습니다. ChatGPT에게도 물어볼까요?
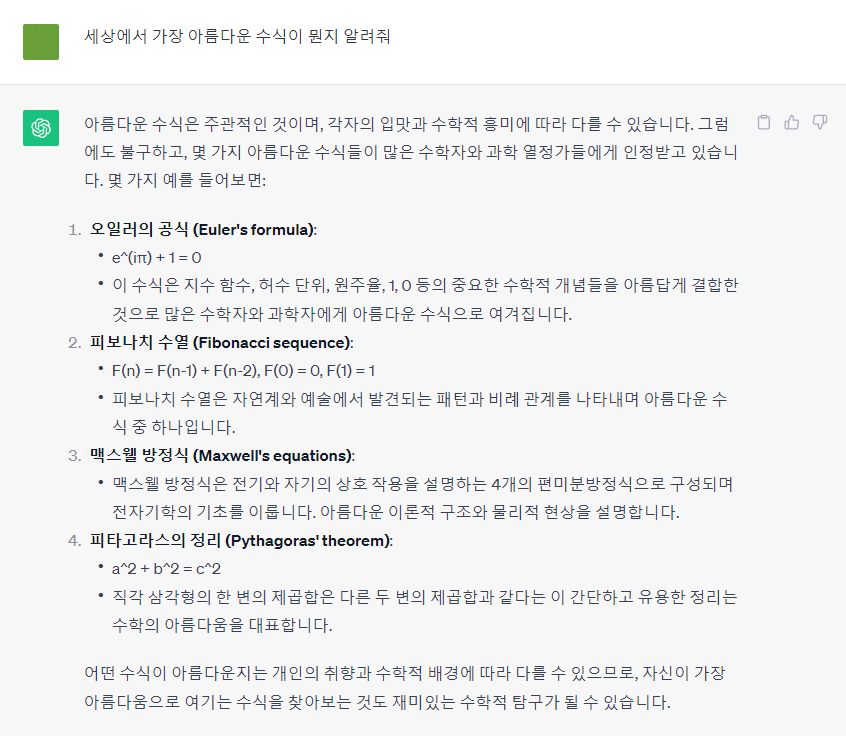
어라, 이 놈도 오일러의 공식을 아름다운 수식으로 뽑네요. 사실 이 수식은 공식이라기보다 등식이라 보는 것이 적합합니다.
그렇다면 갑자기 궁금해집니다. 이 등식이 왜 아름다운 수식인지, 이 수식이 어떻게 나오는지 이해해보겠습니다.
2. 선수학습 요소
① 삼각함수, 지수함수(특히, 자연상수 e)에 대한 이해
② 급수가 무엇인지에 대한 이해
③ 허수단위 i
위의 내용을 모르시는 분들은 (4. 오일러의 공식) 마지막 부분의 결과만 받아들이고 뒤로 넘어가셔도 됩니다!
3. 테일러 급수(Taylor Series)
위 수식을 이해하기 위해서는 여러가지 방법이 있지만 이 글에서는 테일러 급수라는 것을 이용해보려 합니다.
우리가 고등학교에 이르기까지 배운 함수는 일차,이차함수 등의 다항함수, 지수함수, 로그함수, 삼각함수 등이 있습니다.
(공식적 교육과정에 포함되지 않은 가우스 함수([x]) 같은 함수들은 포함하지 않고요.)
배워보신 분들은 알 겁니다. 지수,로그,삼각함수 등의 초월함수들을 다루는 것보다 다항함수를 다루는 것이 훨씬 편하다는 사실을요.
여기서 수학자들이 생각합니다. 초월함수들을 다항함수 꼴로 나타낼 수는 없을까? 나타낼 수 없다면 다항함수에 근사시킬 수 있을까?
그에 대한 해답이 바로 테일러 급수입니다.
테일러 급수에 대한 설명을 하려면 사실 테일러 정리, 나머지항, 수렴구간 등의 이야기를 해야하지만 어렵고 재미 없으니 패스하고,
테일러 급수를 생각하게 된 경위만 설명하겠습니다.
예를 들어, 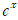 를 다항함수의 합으로 나타낼 수 있다면 어떻게 될까요? 다음처럼 말이죠.
를 다항함수의 합으로 나타낼 수 있다면 어떻게 될까요? 다음처럼 말이죠.

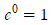 이므로 양변에 x=0을 대입하여
이므로 양변에 x=0을 대입하여 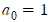 을 얻습니다.
을 얻습니다.
양변을 한 번 미분해보겠습니다.
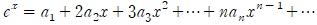
양변에 x=0을 대입하여 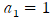 을 얻습니다.
을 얻습니다.
양변을 다시 한 번 미분해보겠습니다.
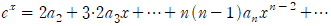
양변에 x=0을 대입하면 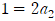 이므로
이므로 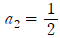 임을 알 수 있습니다.
임을 알 수 있습니다.
한 번만 다시 미분해보겠습니다.
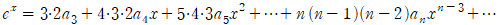
양변에 x=0을 대입하면 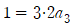 이므로
이므로 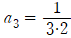 임을 알 수 있습니다.
임을 알 수 있습니다.
슬슬 규칙성이 보이기 시작합니다. 마지막 식에서 (n-3)번 미분하면 어떻게 될까요?
좌변은 그대로 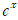 이겠구요, 우변은
이겠구요, 우변은 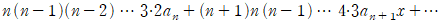 이 될겁니다.
이 될겁니다.
우변의 식이 복잡한 건 상관 없습니다. 중요한건 양변에 x=0을 대입하면 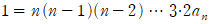 이 되므로
이 되므로
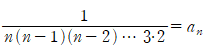 라는 사실이죠.
라는 사실이죠.
그런데, 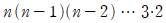 처럼 나열되어 있으니 보기 불편합니다. 우리는 배운 것이 있죠.
처럼 나열되어 있으니 보기 불편합니다. 우리는 배운 것이 있죠.
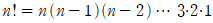 이라 정의하고, n 팩토리얼이라 부르기로 합니다. 또,
이라 정의하고, n 팩토리얼이라 부르기로 합니다. 또, 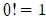 이라 정의합니다.
이라 정의합니다.
그러면
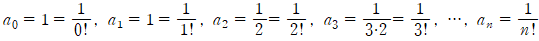
을 얻습니다. 따라서 우리가 구하려고 했던 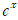 는 다음과 같이 나타낼 수 있습니다.
는 다음과 같이 나타낼 수 있습니다.
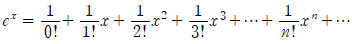
이를 x=0에서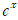 의 테일러 급수, 특히 이는 x=0을 중심으로 했기 때문에 매클로린 급수라고 부릅니다.
의 테일러 급수, 특히 이는 x=0을 중심으로 했기 때문에 매클로린 급수라고 부릅니다.
마찬가지 방법으로 sinx와 cosx의 x=0에서 테일러 급수를 얻을 수 있습니다. 이는 심심하면 직접 해보시길 권유드립니다.
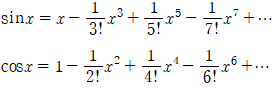
4. 오일러의 공식
위에서 얻은 식
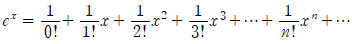
의 양변에 x대신 ix를 대입해보겠습니다. 그러면 다음을 얻습니다.
![]()
![]() 임을 이용하여
임을 이용하여 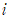 가 붙어있는 항끼리 묶어 정리하면,
가 붙어있는 항끼리 묶어 정리하면,
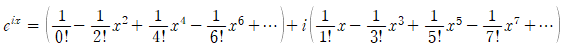
입니다.
위에서 sinx와 cosx의 테일러급수가
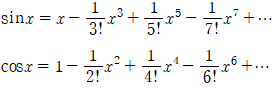
라고 했고, 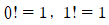 이므로 대입하여 정리하면
이므로 대입하여 정리하면
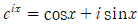 임을 확인할 수 있습니다! 이를 오일러의 공식(Euler's Formula)라고 합니다.
임을 확인할 수 있습니다! 이를 오일러의 공식(Euler's Formula)라고 합니다.
드디어 우리는 오일러의 등식을 증명할 모든 준비가 끝났습니다.
(결과 : 오일러의 공식은 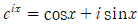 이다.)
이다.)
5. 오일러의 등식
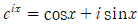 의 양변에
의 양변에 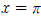 를 대입하면
를 대입하면 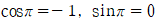 이므로
이므로 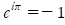 입니다.
입니다.
양변에 1을 더하면 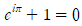 이라는 오일러의 등식을 얻을 수 있습니다.
이라는 오일러의 등식을 얻을 수 있습니다.
제가 어느 대학교 면접에 갔을 때, 앞의 학생이 수학이 아름답다라고 정의 했는데 견해를 밝혀보라는 면접 질문을 받았습니다.
그에 대한 생각은 당연히 한 번도 해보지 않았기에 어버버하고 떨어진 기억이 있는데, 대학교에서 저 등식을 알게 되면서 아쉬웠던 기억이 있습니다. 저 등식을 조금 더 빨리 알았더라면 이야기를 할 수 있지 않았을까..
정말 신기하고 아름답지 않나요? 어떻게 아다리가 잘 맞아서 자연상수 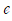 , 원주율
, 원주율 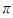 , 허수단위
, 허수단위 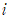 , 곱셈에 관한 항등원 1, 덧셈에 관한 항등원 0이 적절하게 결합하여 하나의 수식을 만들어낸다는게 말이죠.
, 곱셈에 관한 항등원 1, 덧셈에 관한 항등원 0이 적절하게 결합하여 하나의 수식을 만들어낸다는게 말이죠.
6. 오일러의 공식의 활용
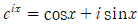 라는 오일러의 공식은 여러 신기한 결과들을 이끌어냅니다.
라는 오일러의 공식은 여러 신기한 결과들을 이끌어냅니다.
① 양변에 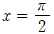 를 대입하면
를 대입하면 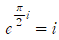 임을 얻을 수 있습니다. 양변에 i제곱을 해봅시다.
임을 얻을 수 있습니다. 양변에 i제곱을 해봅시다.
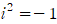 이므로
이므로 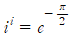 가 됩니다. 허수 i의 i제곱은 허수가 아닌 실수로 나오게 됩니다.
가 됩니다. 허수 i의 i제곱은 허수가 아닌 실수로 나오게 됩니다.
② 이번엔 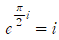 의 양변에 루트를 씌워봅시다. 루트를 씌우는 것은 양변에 1/2 제곱하는 것과 같으므로,
의 양변에 루트를 씌워봅시다. 루트를 씌우는 것은 양변에 1/2 제곱하는 것과 같으므로,
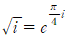 을 얻을 수 있습니다.
을 얻을 수 있습니다. 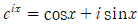 의 양변에
의 양변에 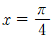 을 대입하면
을 대입하면 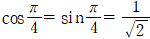 이므로
이므로
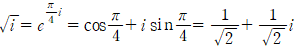 입니다.
입니다.
실제로 우변을 제곱해보면 i가 나옵니다.
7. 세 줄 요약
① 오일러의 등식 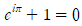 은 e, i, 원주율, 덧셈항등원 0,곱셈항등원 1이 아다리가 잘 맞아서 만들어진 결과물이므로 아름답다.
은 e, i, 원주율, 덧셈항등원 0,곱셈항등원 1이 아다리가 잘 맞아서 만들어진 결과물이므로 아름답다.
② 이건 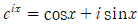 을 유도해서 증명하는데 과정이 굉장히 복잡하다.(사실은 알면 안복잡하다.)
을 유도해서 증명하는데 과정이 굉장히 복잡하다.(사실은 알면 안복잡하다.)
③ 이걸로 신기한 결과들을 얻을 수 있다. (i의 i제곱은 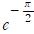 이고, 루트 i는
이고, 루트 i는 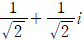 이다.)
이다.)
지금까지 오일러의 등식에 대해 알아보았습니다. 감사합니다.